From: Reese on Play - An Introduction to Good Bridge

The Theory of Symmetry

Terence Reese
Terence Reese
Some players speak of the “Law of Symmetry”, but it is at best only a theory, whose basis is this: that from the character of his own hand pattern a player can draw inferences concerning the patterns of the other hands and of the distribution of the four suits. If a player has four cards of a suit, certain mathematical probabilities can be laid down concerning the likely distribution of the remainder of that four-card suit. Those who have great faith in the theory of symmetry contend that those probabilities are affected by the distribution of the hand in which the four-card suit is held. If you have a common 4-4-3 2 pattern, they say, you are likely to find a similarly balanced remainder for your four-card suits; but if your shape is 7-4-1 1, then the suit in which you hold four cards is likely to be distributed in an unbalanced way throughout the whole deal, say 5-4-3-1, 6-4-2 1, or even 7-4-1 1.

To put this argument at its simplest, the contention is that if you have yourself an unbalanced hand pattern, such as 6-5-1-1, then you are likely to find that your long suits break badly against you.

It must be stated at once that this argument has no support among mathematicians. It is easy to show that if you divide a pack into two halves of twenty-six cards each (which, in effect, is done in every deal), the distribution of the cards among one set of twenty-six cards cannot be affected by the distribution among the other set. Nevertheless it may be that this rationalistic argument oversimplifies the matter. The fact that the shuffle is imperfect gives ground for supposing that mathematical probabilities do not express the true odds in actual play. The opinion of most expert players is that unbalanced patterns do tend to co-exist in one deal. They trust in this to the extent of playing for a 3-1 rather than a 2-2 break when either dummy’s hand or their own is unbalanced. So far as can be judged, experience does support the belief that one singleton is likely to be balanced by another.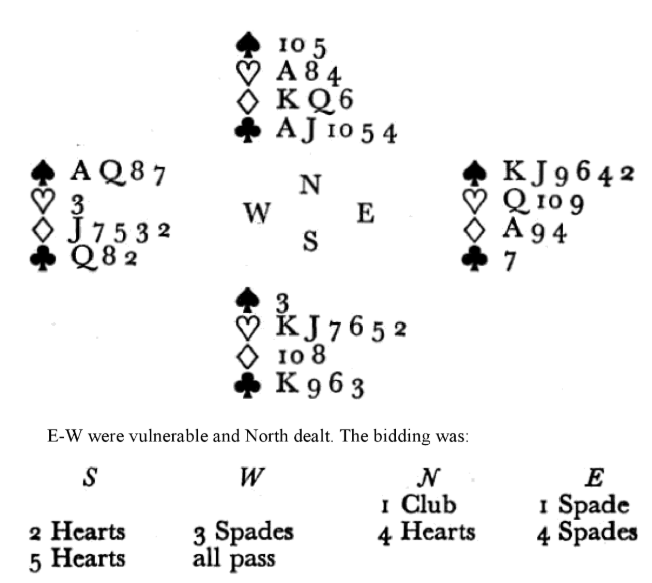 The hand above is an example. The player with firm belief in the theory of symmetry would be influenced to finesse trumps rather than to play for the drop, because his own hand pattern was an unbalanced 6-4-2-1. A more extravagant belief is that a player’s hand pattern is more likely than normal odds suggest to be reflected in the distribution of his long suit throughout the entire deal. If you have a 7-2-2-2 pattern, it is said, you may expect the remainder of your 7-card suit to be divided 2-2-2 among the other hands. There are opportunities for research on this subject. The conclusion is this:

When the odds are mathematically very close, as they are when it comes to finessing or playing for the drop of the Queen with nine cards, symmetry is a better guide than nothing.

If there are singletons about, then it may be best to play for a 3-1 division.

Don’t forget to follow us @

 

RELATED ARTICLESMORE FROM AUTHOR