Source: Article written by T.C. Pant, for the Delhi Bridge Association
Every good Bridge player knows that a Bridge hand is made of either 3 odd & 1 even OR 3 even & 1 odd combination i.e. the 13 cards in a hand will be either distributed in patterns like 4-3-3-3, 5-3-3-2, 6-3-3-1 (3 sets of odd & 1 set of even) or 4- 4-3-2, 6-4-2-1, 5-4-2-2 (3 sets of even & 1 set of odd).
Based on this knowledge, I have tried to develop a theory for finding patterns of a Bridge hand and have reached to the following conclusion:
As you already know yours as well as Dummy’s hand pattern, hence while playing the hand, if you are able to count the pattern of one of your opponent, then the hand pattern of the other opponent can also be found out with a “High probability”.
When there are not enough clues available, all good Bridge players consider “probability” as an important weapon for fulfilling their contracts. You can always hear Bridge players talking that they took finesse, as the probability of taking finesse was higher than the probability of the suit dividing in a certain fashion or vice versa. Hence my theory of finding the hand pattern and hence the distribution of the opponent’s hand is also based on the higher probability of hands, which get dealt in a certain pattern.
For easiness of reference, we will call a “3 odd & 1 even” pattern hand as “ODD” and a “3 even & 1 odd” pattern as “EVEN” pattern hand.
For coming to conclusions on my theory, I generated 2000 hands using the deal generator program BIGDEAL, which was used at Maastricht Olympiad. The idea was to find the patterns of these hands. The statistics of hand patterns came out as follows:
• 627 hands were generated, with 3 ODD & 1 EVEN pattern
• 634 hands were generated, with 3 EVEN & 1 ODD pattern
• 558 hands were generated, with 2 EVEN & 2 ODD pattern
• 85 hands were generated, with all 4 EVEN patterns
• 96 hands were generated with all 4 ODD patterns
Hence hands having 3 patterns of one type & 1 of another type (3 ODD & 1 EVEN OR 3 EVEN & 1 ODD) occurred 627+634 = 1261 times out of 2000 (63%). Hands with 2 ODD & 2 EVEN patterns occurred 558 times out of 2000 (28%) and hands with all ODD or all EVEN patterns occurred 181 times of 2000 (9%).
I have generated many more hands and found out that the 3 ODD & 1 EVEN OR 3 EVEN & 1 ODD pattern occurs with a probability of 0.62 to 0.68. Even if you try it randomly on a Bridge book or magazine you will find that more than 62% hands follow this pattern.
From above, we can conclude that if your and your partner’s hand pattern is ODD and while playing the hand you are able to find out that one of your opponent’s hand also have an ODD pattern, then you have around 62% chance that the other opponent will have EVEN pattern. Similarly if you & your partner and one of the opponents have EVEN pattern then there is 62% chance that the 4th hand will follow a ODD pattern.
In fact as the probability that the fourth hand will turn out to be of same pattern as the other three hands i.e. all ODD or all EVEN is only 0.09 (90 hands out of 1000), hence we can even say that “If the three hand patterns are same, then the probability that the fourth hand will be of different pattern is as high as 90%”
Only in cases, where the declarer has counted 2 hands of one pattern and the third of different pattern, he will require better judgment for finding the pattern of 4th hand, as the probability that the fourth hand pattern does not go along with my theory is 28.9% (2 Even & 2 Odd pattern combination). However, this case also gives you a 71% probability of success in estimating the pattern of 4th hand.
I have tried this theory practically on table and will like to give an example of one of the hands, which came across in Delhi Bridge Association’s weekly Pairs tournament.
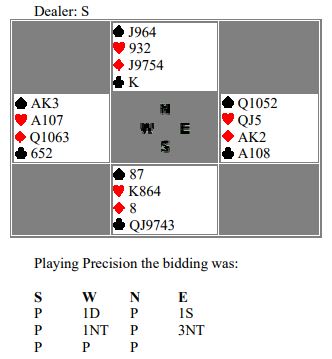
North lead his 4th best Diamond, won by West with
10. When West played a low diamond to his Ace, South showed out. The
Q was finessed and
J continued, covered by King and taken by Ace. Declarer trying for a Spade & Club squeeze now rectified the count by playing a low club and ducking (in last 4 card position, South with 5 Clubs & 4 Spades will get squeezed when 3 Hearts, 4 Diamonds & 2 clubs are played). North continued with diamonds. When declarer played the
A, North showed out.
The inference up to now is that North has the ODD pattern (as already 2 odd distribution have occurred and hand can only be either 3 odd – 1 even or 3 even – 1odd). He has 5 diamonds & 1 club and has already followed to 2 Hearts. Similarly we know that South has 6 Clubs & 1 Diamond and has followed to 2 Hearts. When you cash the
A and both follow, you have a big GUESS?
Is North having 4 Hearts & 3 Spades or 3 Hearts & 4 Spades. I went along with my theory. Myself, my partner and my left opponent have ODD pattern. Hence with as high as 90% probability South should have EVEN pattern. As South has already shown 6 clubs, 3 Hearts & 1 Diamond, the only combination to make his hand an EVEN pattern can be 6 Clubs, 1 Diamond, 4 Hearts & 2 Spades. Hence when both followed to my
A &
K, I coolly took the spade finesse, when North played low to my third spade, making 12 tricks and getting a TOP.
To sum it all, probability is probability and the theory may fail more than once. However, it is a fact that more often than required, the Bridge players then also go for the finesse, which has only 50% probability of success. If that is so, why not to take chances with my theory which has far more probability of success, in finding the hand patterns, which may help you in squeezing, end playing, playing for a drop and other juggleries of Bridge.
Just try this out? It will be real fun.
Don’t forget to follow us @
