Source: Wikipedia
In contract bridge, the
principle of restricted choice states that play of a particular card decreases the probability its player holds any equivalent card. For example, South leads a low spade, West plays a low one, North plays the queen, East wins with the king. The ace and king are equivalent cards; East’s play of the king decreases the probability East holds the ace – and increases the probability West holds the ace.
The principle helps other players infer the locations of unobserved equivalent cards such as that spade ace after observing the king. The increase or decrease in probability is an example of Bayesian updating as evidence accumulates and particular applications of restricted choice are similar to the Monty Hall problem.
Jeff Rubens (1964, 457) stated the principle thus: “The play of a card which may have been selected as a choice of equal plays increases the chance that the player started with a holding in which his choice was restricted.”
Crucially, it helps play “in situations which used to be thought of as guesswork.” In many of those situations the rule derived from the principle is to
play for split honors. After observing one equivalent card, that is, one should continue play as if two equivalents were split between the opposing players, so that there was no choice about which one to play. Whoever played the first one doesn’t have the other one.
When the number of equivalent cards is greater than two, the principle is complicated because their equivalence may not be manifest. When one partner holds
Q and
10, say, and the other holds
J, it is usually true that those three cards are equivalent but the one who holds two of them does not know it. Restricted choice is always introduced in terms of two touching cards – consecutive ranks in the same suit, such as ♥QJ or ♦KQ – where equivalence is manifest.
If there is no reason to prefer a specific card (for example to signal to partner), a player holding two or more equivalent cards should sometimes randomize their order of play (see the note on Nash equilibrium). The probability calculations in coverage of restricted choice often take uniform randomization for granted but that is problematic.
The principle of restricted choice even applies to an opponent’s choice of an opening lead from equivalent suits. See Kelsey & Glauert (1980).
Example
 A J 10 9 6 |
| 8 7 5 4 |
Consider the suit combination represented in the figure. There are four spade cards
8 7 5 4 in the South (closed hand) and five
A J 10 9 6 in the North (dummy, visible to all players).
West and East hold the other four spades:
K Q 3 2 in their two closed hands.
South leads a small spade, West plays the 2 or 3, dummy North plays the
J, and East wins with the
K. Later South leads another small spade and West follows low again. Now only one spade card is “unknown” to South, not yet observed or inferred, with North and East yet to play on the second spade trick. Is it better to play
A, hoping to drop
Q from East, or to finesse again with
10, hoping to drop
Q from West on the third round of the suit? That is, should declarer play for the defenders’ original holdings to be 3 2 and K Q or Q 3 2 and K?
The principle of restricted choice explains why the latter is now about twice as likely, so that to finesse again by playing
10 is nearly twice as likely to succeed.
Prior to play, 16 possible West and East spade holdings or “lies” are possible from the perspective of South. These are listed at left, ordered first by “split” from equal to unequal numbers of cards, then by West’s holding from strongest to weakest.
After West follows to the second spade, which is the moment of decision referred to above, only two of 16 original lies remain possible (bold), for West has played both low cards and East the king. At first glance, it may seem that the odds are now even, 1:1, so that South should expect to do equally well with either of the two possible continuations.
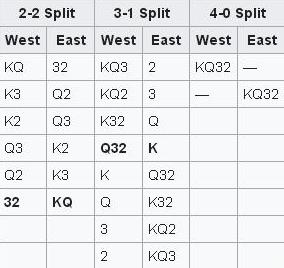
However, this is not the case because if East had
K Q, he could equally well have played the queen instead of the king. Thus some deals with original lie 32 and KQ would not reach this stage; they would instead reach the parallel stage with
K alone missing, South having observed 3 2 and Q. In contrast, every deal with original lie Q 3 2 and K would reach this stage, for East played the king perforce (without choice, or by “restricted choice”).
If East would win the first trick with the king or queen
uniformly at random from
K Q, then that original lie 3 2 and K Q would reach this stage half the time and would take the other fork in the road half the time. Thus on the actual sequence of play, the odds are not even but one-half to one, or 1:2. East would retain queen from original
K Q about one-third of the time and retain no spades from original
K about two-thirds of the time.
Importantly, this assumes that the defenders have no signalling system, so that the play by west of (say) the 3 followed by the 2 does not signal a doubleton. During the course of many equivalent deals, East with
K Q should in theory win the first trick with the king or queen uniformly at random; that is, half each without any pattern.
