Source:
wimpy-bridge by Jim Diebel




In
past articles, I have been promoting the advantages of raising Partner’s 1
st response of 1 in a major with only 3 card support, assuming you (Opener) have a ruffing value somewhere. Although the advantages outweigh the disadvantages by a wide margin, there are still going to occasionally be some hands where someone is going to have to play in a 4-3 trump fit. To understand the difference between playing in an 8 or 9 card fit and playing in a 7 card fit, we need to have a short discussion of basic probability.
When you hold 9 combined cards in a suit, (4 outstanding) the missing cards will split:
2-2 40% of the time
3-1 50% of the time
4-0 10% of the time
When you hold 8 combined cards in a suit, (5 outstanding) the missing cards will split:
3-2 68% of the time
4-1 28% of the time
5-0 4% of the time
When you hold 7 combined cards in a suit, (6 outstanding) the missing cards will split:
3-3 36% of the time
4-2 48% of the time
5-1 15% of the time
6-0 1% of the time
Examination of the above statistics lead us to a few critical conclusions. First, when there are an
odd number of cards outstanding, the suit is most likely to break evenly (closely). When there are an
even number of cards outstanding, the suit is most likely
not to break evenly. Therefore, when playing in an 8-card trump fit, we can expect that the missing trumps will break 3-2 about two-thirds of the time. If our contract hinges on the trump suit breaking well, we have a decent chance.
Alternatively, when playing in a 4-3 trump fit, we must assume that the trumps will break 4-2. Naturally, if the only chance we have to make our contract is a 3-3 trump division, we’ll play for it, knowing that it’s only going to happen about one-third of the time. However, if we can come up with a plan to cope with a possible 4-2 trump break, we will be successful a whopping 84% (48% + 36%) of the time.
This translates into the most general principle in playing a 4-3 trump fit:
You must resist trumping from the 4-card holding. If you do, (since one of the opponents rates to hold 4 trumps), you will often lose control of the hand.
Both Sides Vul
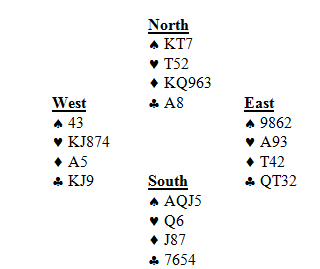
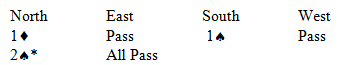
*better bid than 1NT or 2

West leads the

7 against 2

. East wins the

A and returns the

9. West wins and continues with the

J.
South must resist the temptation to trump the 3
rd heart, and instead pitch a club. West can not profitably continue hearts, so switches to a club. South calls for the

A from dummy and must knock out the

A before drawing trumps.
As the cards lie, South cannot lose more than 3 hearts, 1 club and 1 diamond. If he carelessly trumps the 3
rd heart, when he attempts to draw trumps, East will remain with a long spade and will ruff in on a diamond trick. After that, the defense will take the rest of the tricks. South will likely end up down 2. Note that 1NT would fare no better. The defense would take the first 5 heart tricks and switch to a club. The defense will score 5 hearts, 3 clubs and a diamond for down 3 unless South cashes out his 5 tricks to get out for down 2.
Both Sides Vul
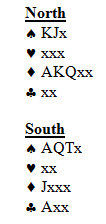

* Support double (3 card support)
** Do something intelligent
South is an experienced player and chooses to play in a known 4-3 spade game instead of the easier 5

. In 5

, North will score 5 diamonds, 4 spades, 1 club, and an eventual heart ruff in dummy. (After drawing trumps, North will pitch a club on the 4
th spade.) In 4

, South must exercise more caution. The defense starts with 3 rounds of hearts, and South simply pitches a club from hand. The defense has no reply. South can draw 4 rounds of trumps, and come to 10 tricks. If South ruffs the 3
rd heart, the likely 4-2 trump split may doom the contract. The defender with 4 trumps will trump the 4
th diamond lead and play another heart. No matter which hand ruffs the heart, South will be unable to both draw the last trump an enjoy the 5
th diamond. South gets a well earned top for 620.

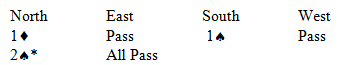 *better bid than 1NT or 2
*better bid than 1NT or 2
 * Support double (3 card support)
** Do something intelligent
South is an experienced player and chooses to play in a known 4-3 spade game instead of the easier 5
* Support double (3 card support)
** Do something intelligent
South is an experienced player and chooses to play in a known 4-3 spade game instead of the easier 5
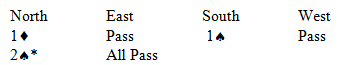 *better bid than 1NT or 2
*better bid than 1NT or 2
 * Support double (3 card support)
** Do something intelligent
South is an experienced player and chooses to play in a known 4-3 spade game instead of the easier 5
* Support double (3 card support)
** Do something intelligent
South is an experienced player and chooses to play in a known 4-3 spade game instead of the easier 5